卒研の経緯

NLP2023 で発表した『自己注意機構における注意の集中が相対位置に依存する仕組み (pdf)（以後、当研究）』は、いろいろと試行錯誤した末の着地点だけを述べていて、そういえばそこに至った経緯に触れていなかったので、卒研と学会を懐かしみながら書きました。（26 min Read は草。）

自分の研究”だけ”に向き合っていると気づかなかったが、自分の分析方針はどうやら異質らしい。（自覚している範囲だと）下の 3 点が異質に感じる。

そもそも軸が違う
文章表現の周波数領域について分析している
データではなくパラメータに対して特異値分解をしている
etc.

このそれぞれについて（etc. も含めて）4 セクションを分けて「なぜそうしたのか」を振り返る。

そもそも軸が違う

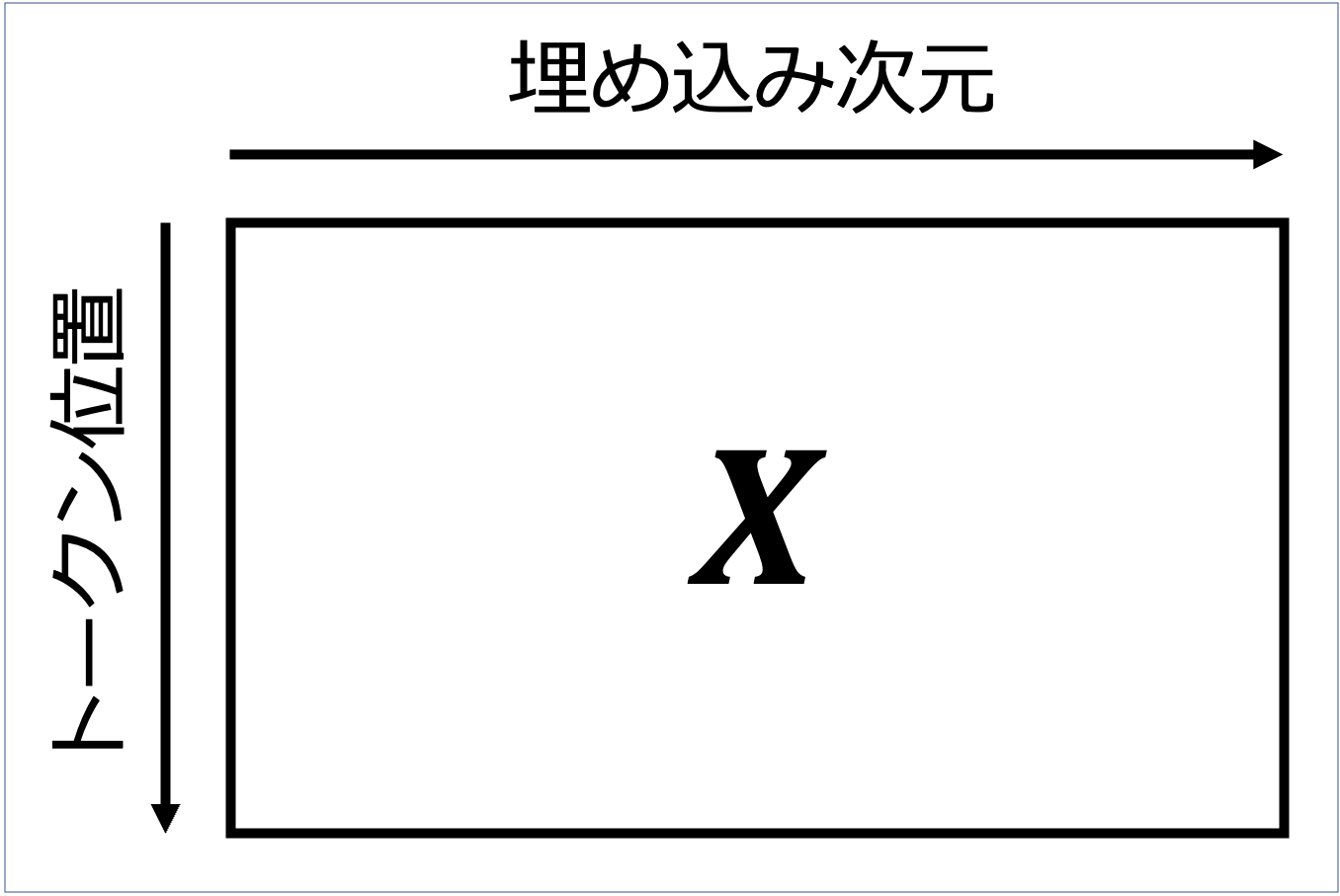
埋め込み表現の分野をざっくりと言い表すと、入力や出力やモデル内部から得られる埋め込み行列 $X$ の分析をしている。本記事では、この $X$ を下図のように定義する。

脱線

このブログの fork 元のデモを久しぶりに見たら、画像を回り込んで文章が書ける機能が追加されていた。反映したいけど merge しようとしたら conflict 大量発生して奇声あげそうなので保留…

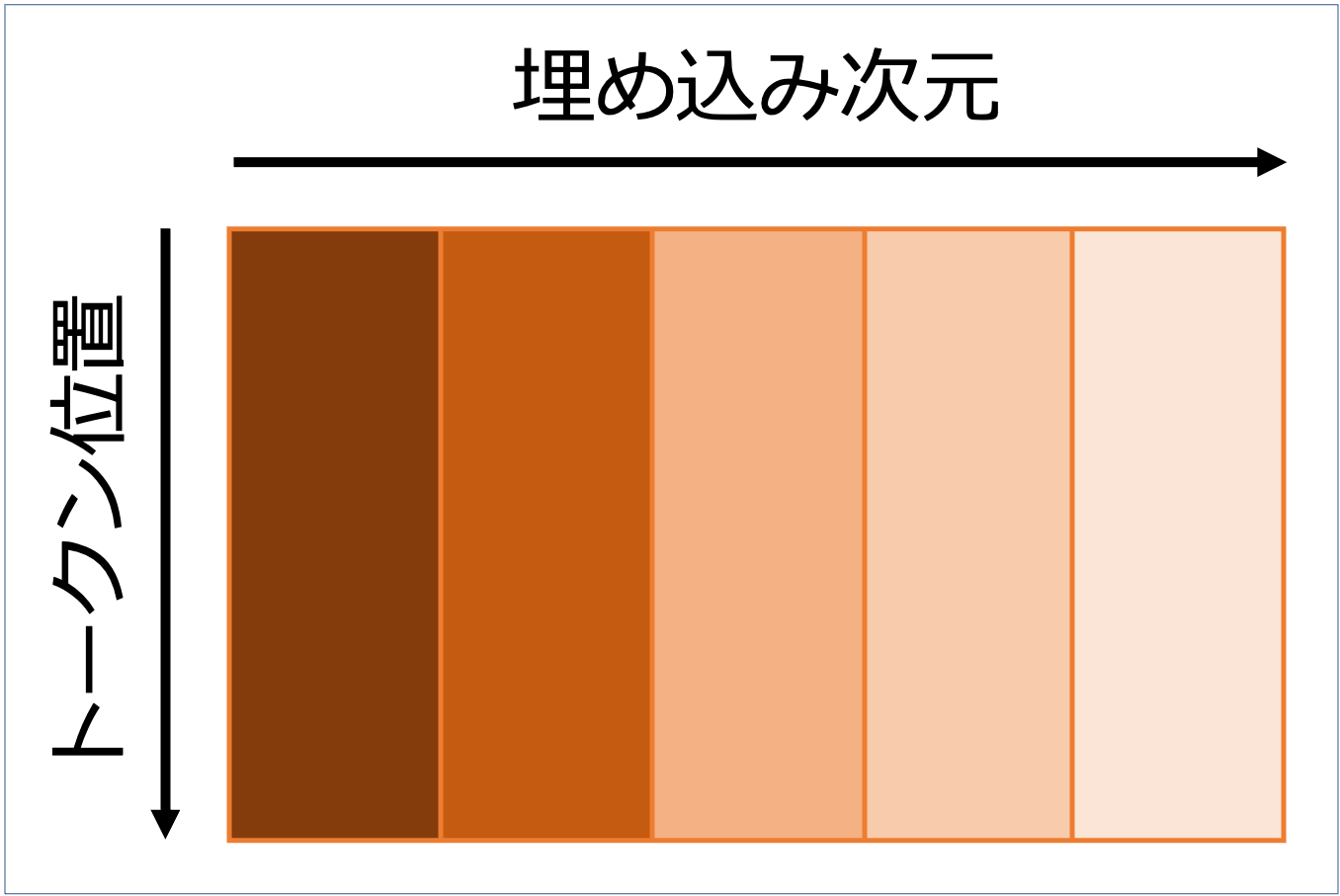
例えば、["I", "will", "be", "back", "!"] というトークン列を埋め込み行列 $X$ で考えると、"be" の埋め込み表現は $X$ の 3 行目に対応する。一般的な研究では、単語に対応する埋め込みである各行について分析が行われている。

しかし、当研究は位置に興味があったので、行分解して文をバラバラの単語にするのではなく列で分解した。

これが一般的な方針と異なる理由だ。（正直、これはそこまで変なことをしているわけではないとは思う。）

文章表現の周波数領域について分析している

この見出しだけ見ると変態の所業に感じる。ただし、文章が時系列データだと抽象的に考えると、これも別にそこまで変態ではないはず。

時系列データとは内容だけでなくその順番にも意味があるデータのことを指す。時系列データであるか否かは、データをシャッフルしていいかを考えると簡単に判定できる。例えば、音楽などはシャッフルしたらデータの意味が崩壊してしまう。

では、文章はどうか。音楽のドレミと異なり、単語には重要度に差があるので、 bag-of-words のように順番を無視しても推論できちゃったりするが、高精度を出すには単語の順序、つまり、文脈を捉える必要が出てくる。したがって、文章は時系列データの一種である。

すると、音楽や音声などを扱う信号処理分野で日常的に行われるフーリエ変換を埋め込み行列 $X$ の列方向に適用するのも、変わっているかも知れないが荒唐無稽ではないだろう。

（学会発表で振幅スペクトルの話の導入に、この辺のお気持ちを述べるべきだったと反省。）

データではなくパラメータに対して特異値分解をしている

特異値分解（SVD）は主成分分析（PCA）とほぼ同じようなもんらしいので¹、見出しを「データではなくパラメータに対して PCA をしている」に変えてみる。すると、一気に変態な見出しになった。

普通、 PCA といえば下の例のように、データ に対して行われる。

5 教科のテストの点数を PCA すると、理系っぽさと解釈できる主成分ベクトルが得られた。
- 多分、数学 + 理科 - 国語 - 社会 みたいな感じのベクトルになると思う。
word2vec の単語埋め込みを PCA すると、第 1 主成分が頻度、第 2 主成分が品詞とそれぞれ解釈できそうなベクトルが得られた。

しかし、今回の対象はパラメータだから「？」となってしまう。このセクションの経緯を説明するのが一番難しいのでいくつかのサブセクションに分ける。

初期目標: 中間層から位置埋め込み由来の成分を取り出す

まず、最初はもちろん（パラメータではなくデータである）埋め込み行列 $X$ に対して PCA をして、位置表現のような主成分を得ようとした。他にも、音源分離に使われる独立成分分析（ICA）も試したりした（参考）²³。

このへんは ‘23 年度の夏休み前にしていたのであまり覚えていないが、別に PCA でも入力層付近ならそれっぽい成分を抽出することはできていた。ただ、あくまで「それっぽさ」までしか得られないので、胸張って「抽出できました！卒研終了！！」みたいな雰囲気ではなかった⁴。

最終目標: 位置埋め込み由来の成分が文脈に従った推論に寄与することを示す

おそらくこのもやもやした気持ちの原因は、PCA を使って初期目標を達成したとしても最終目標は 1mm も達成できないことに薄々気づいていたからだと思う⁵。

仮に、PCA で位置埋め込みに由来する成分をほぼ完璧に抽出できたとする。しかし、その結果は PCA が文脈理解に必要な成分を抽出できることを示しただけで、文脈を捉える役目の自己注意機構がそれをできるかとは全く関係ない。

静と動

（このセクションを書いていて、自分ってこういうことに興味があったんだということに気づかされた。）

この研究で示したいのは「埋め込みに〇〇という性質が存在する」という状態ではなく、「モデルが〇〇できる」という動作の方だった。すると、分析対象とすべきなのは埋め込み行列 $X$ ではなくパラメータの方ではないか。

PCA は単純に入力 $X$ を直交変換して出力 $Y$ を計算する。（つまり、基底の取り替えにより視点を変えるだけで、データ $X$ を崩すようなことはしない。）すなわち、パラメータを直交行列 $U$ とおくと

\[Y = XU \tag{a}\]

のようにとても単純に書ける。この解釈性の良さのおかげで PCA は重宝されている。

あれなんかこの形見たことあるな。

\[Q = XW^Q,~K=XW^K \tag{b}\]

クエリとキーですね。もしかして、PCA とか ICA とか面倒なことしなくてもクエリとキーをそのまま可視化すると実は面白い形をしてたりして…？⁶

これがマジでした（位置に関して推論するために位置に関する成分を抽出する必要があるので納得はできる）。クエリとキーにバンドパスフィルタをかけてバイアスやノイズっぽいものを除くとよりきれいな形が見えてくる。このノイズはおそらく単語埋め込み由来の成分だと考えられる⁷。

つまり、フィルタリング前は各次元に位置表現と単語表現が混在している。ならば、基底の取り替えれば位置表現だけが抽出できるのではないか。

表現が混在するとは

NLP における埋め込み表現に関わらず、深層学習全般のニューラル表現分析でもこのような話は出てくる。例えば、画像分類モデルのある層において、5 個のニューロンが 形, 色, 明るさ という 3 つの特徴を学習していたとする。じゃあ、1 番目のニューロンが 形 を捉えていて、2 番目のニューロンが 色 を捉えていて、なんてことはなく複数の特徴はいくつかのニューロンに散らばっている。

そこで、1 つのニューロンが 1 つの特徴を推論しているかのようにうまく表現を整理できれば、解釈性が大きく向上する。表現分析の目的は解釈性を向上させることなので、整理のためにエグい手法を使うことはおそらく少なく、分かりやすい単純な直交変換などが好まれる。

特異値分解（SVD）の導入

論文にも記載したが、クエリとキーの積 $QK^T$ を計算するときに $W^Q(W^K)^T$ を計算するため、パラメータ行列は 2 つあるように見えて実は 1 つの行列を分解したものである。もし、

\[\begin{aligned} W^Q &\leftarrow W^Q(W^K)^T \\ W^K &\leftarrow I \end{aligned}\]

のようにパラメータを置き換えても $QK^T$ は全く変わらない。つまり、クエリとキーはパラメータが混ざり合っていて、はっきりとした境界が存在しないため、お互いが独立した概念ではない。（例えば、クエリ $Q$ を作る重要な成分が $W^K$ にあり、その逆もあるかもしれない。）そのため、式 (a) と式 (b) は形は似ているが、$W^Q,~W^K$ 自体は特徴を抽出しているとは言えない。

ここでの目標は

\[Q = XU^Q,~K=XU^K\]

における、PCA のパラメータ行列のような $U^Q,~U^K$ を得ることである。そして、PCA と同じく $U^Q,~U^K$ が直交行列として得られたらより嬉しい。

ここで、SVD を用いると

\[W^Q(W^K)^T = U^Q S (U^K)^T\]

とパラメータが分解されて直交行列である左右特異ベクトルが得られる。この $U^Q,~U^K$ を $X$ に書けたものを可視化すると欲しかった表現が得られた。 SVD でなぜうまくいくのかははっきりとは分からない。まあ、PCA や t-sne で表現が分かりやすくなることもあればそうでないこともあるのでそんなもんなのだろう。

セクションまとめ

このセクションのはじめに「データではなくパラメータに対して PCA をしている」という発言をしたが、これは自分のお気持ちとは全く異なる（数式ではそう見えちゃうけど）。

やりたかったことは、一般的なケースと同じく、データ $X$ に対して基底変換をして解釈しやすい表現を得ることである。そのための変換行列 $U$ は §最終目標でも触れた通り、パラメータ $W$ から得たかった。そこで $W$ から $U$ を得る過程で特異値分解を用いた。

つまり、パラメータを基底変換することで、重要なパラメータの軸やその寄与度が欲しいというお気持ちはなく、普通に混じった表現を特徴ごとに分けたくて、その過程で SVD が有効だった。

そもそも $W^Q(W^K)$ という混ざったパラメータが Transformer 以外でほぼ見かけないので、パラメータを整理するという発想も受け入れ難いのかもしれない。

etc.

クエリとキーは個別に考えられないと言ったそばから分解するのはなぜ

一言でいうと、クエリとキーを個別に考えたかったから（考えられない ≠ 考えてはいけない）。クエリとキーの積を一つの塊として扱うと、ほぼほぼアテンション重み $A$ と同じ行列になってしまう⁸。

自分の興味は「このヘッドでは位置を見てるね」「このヘッドでは係り受けを推論しているね」という結果を知ることではなく、「どうやって位置を見ているんだろう」「どうやって係り先を特定できるのだろう」という操作の方にある。

この立場だと、アテンション重み $A$ はパラメータが色々操作した結果として得られた行列でしかない。なので、そうなった経緯を知るためには分解したくなる。

入力: 埋め込み行列 $X$
途中経過: クエリ $Q$, キー $K$ （← ここが見たい）
観察結果: アテンション重み $A$

埋め込み層だけでなく各層でも直に位置埋め込みを入れたほうがいい？

~~残差接続（Residual Connection）があるので、最終層にも位置埋め込みを直で入力しているとみなせる（多分）。~~

\[\begin{aligned} &\xcancel{X = W + P }\\ &\xcancel{layer_{12}( \cdots (layer_2(layer_1(X) + X) + X) \cdots ) + X} \end{aligned}\]

訂正：こんなに単純な話ではない。

1 層目の Attention の出力 $X$ と埋め込み層の出力 $W+P$ （単語埋め込み $W$ と位置埋め込み $P$ の和）に対する LayerNorm は、位置埋め込み $P$ とその他 $X+W$ の和に適用していると見れる。ここで、その他を無視すると

\[LayerNorm(* + P) = * + SPL\]

と書ける。ただし、$S$ と $L$ はスケールバラメータで対角行列。バイアスは $*$ に吸収させている。つまり、sub-layer を抜けるごとに位置埋め込みの両側の対角行列が増えていくので、$n+1$ 層目の入力は

$layer_{n+1}(* + S_{n}^fS_{n}^a \cdots S_{1}^fS_{1}^a \cdot P \cdot L_{1}^aL_{1}^f \cdots L_{n}^aL_{n}^f )$

みたいな感じになっている（のかな？）。これが正しければ、対角行列の積は対角行列だから結局は最初と同じ

$layer_{n+1}(* + SPL )$

と書ける。

訂正前と大きく違うのは $S~(= \text{diag}(\text{Std}[token_i]))$ が左から掛かってしまうこと。絶対位置埋め込みが周期的なときに、左から行列がかかると、きれいな波形ががったがたになりそう。つまり、$S$ によっては位置埋め込みが壊れて上位層には伝わらなそう。

（訂正部分終了）

なので、モデルの分析をしたときに後層では位置埋め込み由来の成分が目立たない原因は、入力層から上手く伝わっていないのではなく、モデルが捨てていると思われる。

「付き合ってください」って言われた数秒後に「”合” という漢字は 3 文字目だったな」と思うことはないだろう（言われたこと無いから知らんが）。このように後層に行くにつれて位置情報は徐々に不要になり、意味的推論に移行すると考えられる。

編集後記

自分なりの Self Attention の解釈という記事は書き始めから 2 ヶ月経ってるのに 1/3 くらいしか書いてないという怠慢なことをしているので、今回はそうならないように 1 日で一気に書ききった。脳内をかなりさらけ出したので恥ずかしさや怖さを感じている。

https://qiita.com/horiem/items/71380db4b659fb9307b4 ↩
$n$ 個の楽器からなるオーケストラを $d~(\ge n)$ 個のマイクで収録すると $d$ 個の音源ができる。その音源に対して ICA を行うと、楽器ごとの $n$ 個の音源に分離できる（うまくいけば）。 ↩
埋め込み表現だと、$n$ 通りの何らかの価値のある表現を $d$ 次元空間から上手く取り出すという風に言い換えられる。ただし、$n$ は未知なので 1~20 くらいの値で色々試すことになる。 ↩
実際、PCA はそれっぽい軸を得るための手法なので、PCA を使う以上避けては通れない。 ↩
当時はこの言語化できていなかった。 ↩
huggingface を使っている場合、$X$ は output_hidden_states=True とすれば取得できるが、$Q$ や $K$ はちょっとした実装をしないと得られないので、そのまま見たことある人は実はものすごく少ないのではないか。 ↩
どんな文章でもトークンの位置 [1, 2, 3, ...] はもちろん変わらない（当たり前過ぎて逆に変に聞こえるかも）。しかし、happy という単語は文によって 5 番目に現れたり 100 番目に現れたりするので、行列 $X$ の列方向に分析するときはほぼノイズにしか見えない。 ↩
scale や softmax の有無に違いはあるが、どちらも大小関係は変えないので、attention が当たるトークン関係は変わらない。 ↩