今週、PCoA という手法を知り、ちょこちょこ調べていると「非類似度をユークリッド距離とすると、PCoA と PCA は等価になる」という記述をたくさん見ました。 しかし、その証明を見つけられなかったので自分でやりました。
PCoA とは
略さずに書くと Principal Coordinate Analysis (主座標分析) です。 MDS (Multidimensional scaling, 多次元尺度構成法) という手法のうちの一つらしいです。
“〇〇” っていう手法見つけたら “一般化〇〇” っていう手法ありがち
概要を考えるのが面倒なのでアルゴリズムから説明しちゃいます。 記号は wiki と同じです。
1. 非類似度行列 (proximity matrix) を定義する。
非類似度行列を $D$ としたとき、その $(i,j)$ 成分 $d_{ij}$ は、$i$ 番目の観測 $x_i$ と $j$ 番目の観測 $x_j$ の非類似度です。具体例を挙げるならこんな感じ。
| 🍎 | 🍏 | 🍧 | 🍨 | 🍶 | 🍺 | |
|---|---|---|---|---|---|---|
| 🍎 | 0 | - | - | - | - | - |
| 🍏 | 0.1 | 0 | - | - | - | - |
| 🍧 | 0.5 | 0.6 | 0 | - | - | - |
| 🍨 | 0.6 | 0.6 | 0.2 | 0 | - | - |
| 🍶 | 0.8 | 0.7 | 0.8 | 0.9 | 0 | - |
| 🍺 | 0.9 | 1 | 1 | 0.8 | 0.2 | 0 |
非類似度の指標は任意です。ただし、自分自身との非類似度は 0 でなければなりません。
この後の計算に用いるのは、行列 $D$ の各要素を 2 乗した平方非類似度行列 (squared proximity matrix) $D^{(2)}$ です。
\[(D^{(2)})_{ij} = d_{ij}^2\]2. 二重中心化 (double centering)
この処理は初めて知りました。中心化行列 (centering matrix ) $C\in\mathbb{R}^{n\times n}$ を次のように定義します:
\[C = I - \frac{1}{n}\mathbf{1}\mathbf{1}^T\]これを行列 $D^{(2)}$ の両サイドから掛けて:
\[B = -\frac{1}{2} C D^{(2)} C\]とします。すると行列 $B$ の各行和・列和がゼロになるらしいです [参考]。
3. 固有値分解して軸を求める
先ほどの行列 $B$ を固有値分解します:
\[B = V\Lambda V^T.\]この右辺の半分 (?) を計算すると変換後の表現:
\[Y = V\Lambda^{1/2}\]が得られます。
固有値分解くん、線形基底変換系の文脈ではどこにでもいますね。仲良くなりたい。
(個人的) PCA と PCoA の違い
PCA はデータ $X$ から共分散行列 $X^TX$ をつくって、コレを固有値分解します。しかし、PCoA は非類似度行列 $D$ がスタート地点なので、非類似度としていろんな指標を考えることができます。
非類似度 dissim($x_i$, $x_j$) が定義できればいいということは、観測 $x_i$ がベクトルである必要もないのかもしれない。PCoA は次元圧縮としても使われるが、そもそも数空間上になかったものを可視化するという解釈もできるのかもしれない。
本題: $d_{ij} = ||x_i - x_j||$ なら PCoA は PCA
とりあえず、行列 $B=-\frac{1}{2}CD^{(2)}C$ の $(i,j)$ 成分を気合いで求めます。簡略化のために以下の式を定義しておきます。
\[d_{\bullet j}^2 := \frac{1}{n}\sum_i d_{ij}^2, \quad d_{i \bullet}^2 := \frac{1}{n}\sum_j d_{ij}^2, \quad d_{\bullet \bullet}^2 := \frac{1}{n^2}\sum_{i,j} d_{ij}^2\]まず、左側2つの行列の積。
\[(CD^{(2)})_{ij} = \sum_k c_{ik} d_{kj}^2 = \sum_k \left(\delta_{ik} - \frac{1}{n}\right) d_{kj}^2 = d_{ij}^2 - d_{\bullet j}^2\]「知っとるわ」と言われるかもしれないけど、$\delta_{ij}$ は総和 $\sum$ を消してくれるのがポイント。
次に全体。
\[\begin{aligned} (CD^{(2)}C)_{ij} &= \sum_k (d_{ik}^2 - d_{\bullet k}^2) \left( \delta_{kj} - \frac{1}{n} \right) \\ &= d_{ij}^2 - d_{\bullet j}^2 - d_{i\bullet}^2 + d_{\bullet\bullet}^2 \end{aligned}\]なんかこういう式、実験計画法とかでも見たことある気がする
ここで、実際に $d_{ij} = || x_i - x_j ||$ を代入していく。ただし、$x$ は中心化されているとする ( $\sum_i x_i = 0$ )。
1 項目 $d_{ij}^2$:
\[d_{ij}^2 = \| x_i - x_j \|^2 = \|x_i\|^2 + \|x_j\|^2 - 2x_i^Tx_j\]2 項目 $d_{\bullet j}^2$:
\[d_{\bullet j}^2 = \frac{1}{n}\sum_i \left( \|x_i\|^2 + \|x_j\|^2 - 2x_i^Tx_j \right) = \overline{\|x\|^2} + \|x_j\|^2 + 0\]ただし、$\overline{||x||^2} := \frac{1}{n}\sum_i ||x_i||^2$.
3 項目 $d_{i \bullet}^2$:
\[d_{i \bullet}^2 = \frac{1}{n}\sum_j \left( \|x_i\|^2 + \|x_j\|^2 - 2x_i^Tx_j \right) = \|x_i\|^2 + \overline{\|x\|^2} + 0\]4 項目 $d_{\bullet \bullet}^2$:
\[d_{i \bullet}^2 = \frac{1}{n^2}\sum_{i,j} \left( \|x_i\|^2 + \|x_j\|^2 - 2x_i^Tx_j \right) = 2\overline{\|x\|^2} + 0\]全部合わせると:
\[\begin{aligned} (CD^{(2)}C)_{ij} &= (\|x_i\|^2 + \|x_j\|^2 - 2x_i^Tx_j) \\ &- (\overline{\|x\|^2} + \|x_j\|^2) \\ &- (\|x_i\|^2 + \overline{\|x\|^2}) \\ &+ 2\overline{\|x\|^2} \\ &= - 2x_i^Tx_j \end{aligned}\] \[\therefore (B)_{ij} = -\frac{1}{2} (CD^{(2)}C)_{ij} = x_i^Tx_j\] \[\therefore B = X^TX\]あれ、共分散行列になっちゃった。このあと PCoA では、行列 $B$ を固有値分解します。なので、共分散行列に対して固有値分解を行う PCA と等価になります。
実装で確認
固有値分解を用いた PCoA は scikit-bio で利用できます。
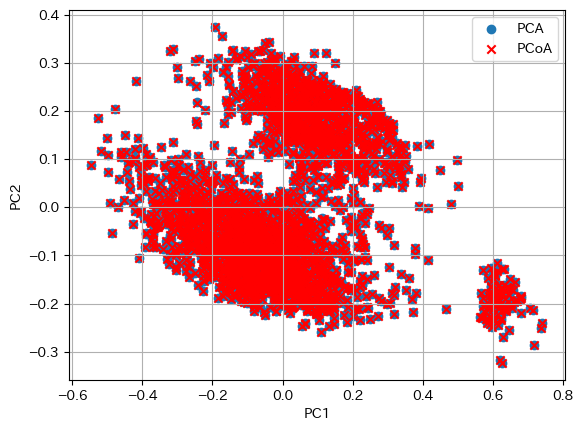
試しに単語埋め込みに対して PCA と PCoA の両方を適用してみましょう。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import plt
from transformers import AutoModel
from skbio.stats.ordination import pcoa
from sklearn.decomposition import PCA
from sklearn.metrics.pairwise import euclidean_distances
model = AutoModel.from_pretrained("bert-base-cased")
we = model.embeddings.word_embeddings.weight.data[1000:4000]
x, y = PCA(2).fit_transform(we).T
plt.scatter(x, y, label="PCA")
x, y = pcoa(euclidean_distances(we)).samples.values.T[:2]
plt.scatter(-x, y, c="r", marker="x", label="PCoA")
plt.xlabel("PC1")
plt.ylabel("PC2")
plt.legend()
わー、一致した。