はじめに
総研大日本語言語科学コースの山本悠士です。
記事（というか備忘録）をちょうど書こうとしていたところで総研大 Advent Calendar のお誘いをいただき、 せっかくの機会なので参加させていただくことにしました。
目的
IBIS2025 にて、2 つの（半）正定値行列の間に Bures 距離 $d$ という尺度があることを知った：
\[d(A, B)^2 = \tr[A] + \tr[B] + -2 \tr[ (A^{1/2} B A^{1/2})^{1/2} ]\]参考：https://arxiv.org/abs/1712.01504
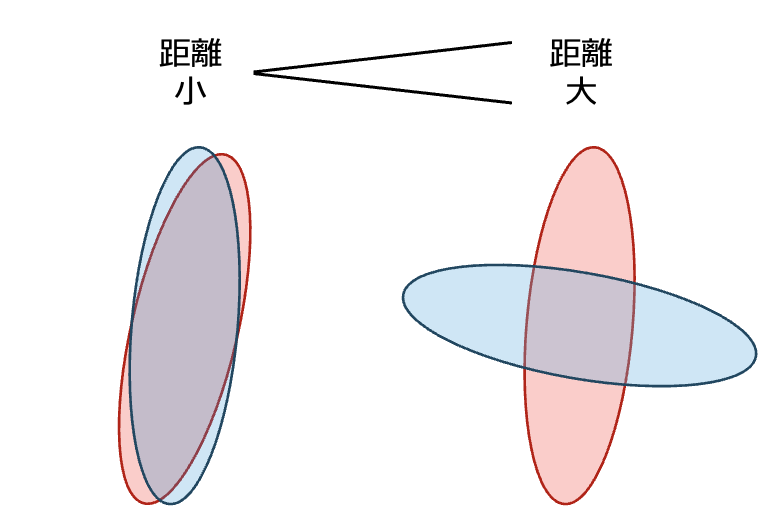
これを使うと例えば正規分布の散らばり方の違いを定量化できる。イメージ図 ↓
しかし、式をぱっと見ただけだとなぜ方向の違いが捉えられるのか分からなかったので、 Gemini と 3 日間会話しながら考えていた。この記事はその備忘録。
おい、ちょっとまて、なぜ日本語言語科学コースの学生が数式をコネコネいじっているんだ？と思った方は研究室のページ https://yokoi-lab.net/research/ も合わせてご覧ください。
極端な例で考えてみる
距離が最小っぽいとき
2 つの正規分布 $\mathcal{N}(a, A), \mathcal{N}(b, B)$ において、 完全に分布の形が重なっているときを考えてみる。 つまり、共分散行列 $A, B$ の各固有ベクトルの方向が一致しているときを考えてみる。
このとき、それぞれの行列は下のように同じ固有ベクトルを並べた行列 $U$ によって対角化される：
\[A = U\Lambda_A U^T, ~ B = U\Lambda_B U^T\]これを $d(A, B)$ の第 3 項の中身に代入すると：
\[\begin{aligned} \tr[ (A^{1/2} B A^{1/2})^{1/2} ] &= \tr[ ((U\Lambda_A U^T)^{1/2} (U\Lambda_B U^T) (U\Lambda_A U^T)^{1/2})^{1/2} ] \\ &= \tr[ ((U\Lambda_A^{1/2} U^T) (U\Lambda_B U^T) (U\Lambda_A^{1/2} U^T))^{1/2} ] \\ &= \tr[ (U\Lambda_A^{1/2} (U^T U)\Lambda_B (U^T U)\Lambda_A^{1/2} U^T)^{1/2} ] \\ &= \tr[ (U\Lambda_A^{1/2} \Lambda_B \Lambda_A^{1/2} U^T)^{1/2} ] \\ &= \tr[ (U (\Lambda_A^{1/2} \Lambda_B \Lambda_A^{1/2})^{1/2} U^T) ] \\ &= \tr[ (U \Lambda_A^{1/2} \Lambda_B^{1/2} U^T) ] \\ &= \tr[ (\Lambda_A^{1/2} \Lambda_B^{1/2} U^TU) ] \\ &= \tr[ (\Lambda_A^{1/2} \Lambda_B^{1/2}) ] \\ &= \sum_i \sqrt{\lambda_{A}^{(i)} \lambda_B^{(i)}} \end{aligned}\]ここで最初の 2 項が $\tr[A] + \tr[B] = \sum_i \lambda_A^{(i)} + \sum_i \lambda_B^{(i)}$ であることと合わせると、
\[d(A, B) = \sum_i \lambda_A^{(i)} + \sum_i \lambda_B^{(i)} -2 \sum_i \sqrt{\lambda_{A}^{(i)} \lambda_B^{(i)}} = \sum_i \left(\sqrt{\lambda_A^{(i)}} - \sqrt{\lambda_B^{(i)}}\right)^2 \ge 0\]（心の声）お、なんか距離っぽくなった。
つまり、散らばりの方向（固有ベクトル）が一致していて、かつ、その散らばり具合（固有値）も一致しているときに $d(A, B) = 0$ となるようだ。
（心の声）なるほど、いかにも直感的。
距離が最大っぽいとき
2 つの正規分布 $\mathcal{N}(a, A), \mathcal{N}(b, B)$ において、 分布の散らばり方が直交しているときを考えてみる。 つまり、共分散行列 $A, B$ の各固有ベクトルの方向が直交しているときを考えてみる。
このとき、それぞれの行列は $U^TV = O$ を満たす行列 $U, V$ によって対角化される：
\[A = U\Lambda_A U^T, ~ B = V\Lambda_B V^T\]これを $d(A, B)$ の第 3 項の中身に代入すると：
\[\begin{aligned} \tr[ (A^{1/2} B A^{1/2})^{1/2} ] &= \tr[ ((U\Lambda_A U^T)^{1/2} (U\Lambda_B U^T) (U\Lambda_A U^T)^{1/2})^{1/2} ] \\ &= \tr[ ((U\Lambda_A^{1/2} U^T) (U\Lambda_B U^T) (U\Lambda_A^{1/2} U^T))^{1/2} ] \\ &= \tr[ (U\Lambda_A^{1/2} (U^T V)\Lambda_B (U^T V)\Lambda_A^{1/2} U^T)^{1/2} ] \\ &= \tr[ (U\Lambda_A^{1/2} O \Lambda_B O \Lambda_A^{1/2} U^T)^{1/2} ] \\ &= 0 \end{aligned}\]負の項が 0 になった。いかにも最大っぽい。
整理
$d(A, B)$ において、 2 項目までは $A$ と $B$ が相互作用しないので置いといて、 第 3 項が分布の形の近さ・遠さを決定づけているようだ。
これまでより、次の不等式が成り立つっぽいという予想が立った。
\[0 \le \tr[ (A^{1/2} B A^{1/2})^{1/2} ] \le \sum_i \sqrt{\lambda_{A}^{(i)} \lambda_B^{(i)}}\]最後にこれを示したい。なお自力では無理だったので Gemini に協力してもらった。
下限の証明
まず、行列 $C = A^{1/2}BA^{1/2}$ をおき、これが半正定値行列であることを示す。
任意のベクトル $x$ について
\[\begin{align*} x^TCx &= x^T A^{1/2}BA^{1/2} x \\ &= (x A^{1/2})^T B(A^{1/2} x)\\ &\ge 0 \end{align*}\]最後に行列 $B$ が半正定値行列だから任意のベクトル $A^{1/2}x$ に対して非負であることを用いた。
したがって、行列 $C$ は半正定値行列だから各固有値 $\lambda_C^{(i)}$ について $\lambda_C^{(i)}\ge 0$。 もちろん、$\sqrt{\lambda_C^{(i)}}\ge 0$も成り立つ。 これより、$\tr[C^{1/2}] = \sum_i \sqrt{\lambda_C^{(i)}} \ge 0$ が成り立つ。
行列の平方根取っている時点で $\ge 0$ って仮定されているのかな
上限の証明
こっちもすんなり示せたと思ったら、Gemini の発言に誤りがあることが発覚し、 真面目にやるとめちゃくちゃむずいことが分かった。 厳密に証明するには von Neumann のトレース不等式 といういかつい道具が必要らしい
すみません、Gemini と会話しても証明できませんでした。 （正しく言うと、Gemini が出してくる証明が正しいと判断できる知識が自分になかった。）
自己紹介
オチがつかなかったので少し自己紹介して終わることにします。
博士進学後に「あなたは何をされている方なの？」というシーンが何度もあったのだが、毎回これにうまく答えられていない気がするので、この場を借りて練習します。
自分の（これまでの）研究のゴールは、一言でいうなら 言語モデルがどのようにテキストを扱っているのかをアルゴリズム的に理解すること です。 野心的に言い換えると、言語モデルの各パラメータが持つ役割をすべて理解することがゴールです。
具体例を使って、山本はどこまで理解したいのかを説明します。 「あけまして」と言われたら一般人は「おめでとう」を想起します。これは日本語でよく学習された言語モデルでも同様のことができます。 しかし、言語モデルはなぜ「おめでとう」を想起できるのでしょうか。
回答の一つとして、「あけまして」の後に「おめでとう」が出現する確率がとても高いという統計情報を学習したから、というのが挙げられます。 しかし、これは言語モデルが「何をしたのか」というエンジニアリングの答えであって、 「なぜできるのか」というサイエンスの疑問までは答えられていないような気がします。 山本は「その統計情報はモデルのどこのパラメータに保存されているのか」「その保存された情報はどのパラメータによって想起に利用されるのか」という疑問を抱きます。
どこに保存し、何を使って想起するのか、といった言語モデルがテキストを扱う際に取りうる計算手順、すなわち アルゴリズム を理解したいというのが自分のゴールです。
立ち話だとこのくらいが良い分量かな。
なんでこんなことに疑問を持つようになったんだろう（自問自答開始）。
人間が蓄積したデータを AI などの機械が学習すると、人間の知的活動が機械の中に表現される。 その機械の中を覗けば知的活動が何だったのかを数式をつかって記述できてしまうのではないか。 みたいなことを想像しているのかなァ。
面白そうだけど簡単には理解できないものが好きなのかも。 この記事も学会中に出会った面白そうだけど理解できない数式を見たのがきっかけで書いている。 言語モデルもブラックボックスなんて言われたりするけど、その箱には鍵がかかっているわけではなくただ理解するのが難しいだけ。その中身では言語が数学的に処理されているという事実にどこかのタイミングで興奮してしまい、箱を開けて覗き込むのが趣味になってしまったのだろう。
最後までお付き合いいただきありがとうございました。 明日はクリスマスイブですね。 まえやまさんの記事をお楽しみに。